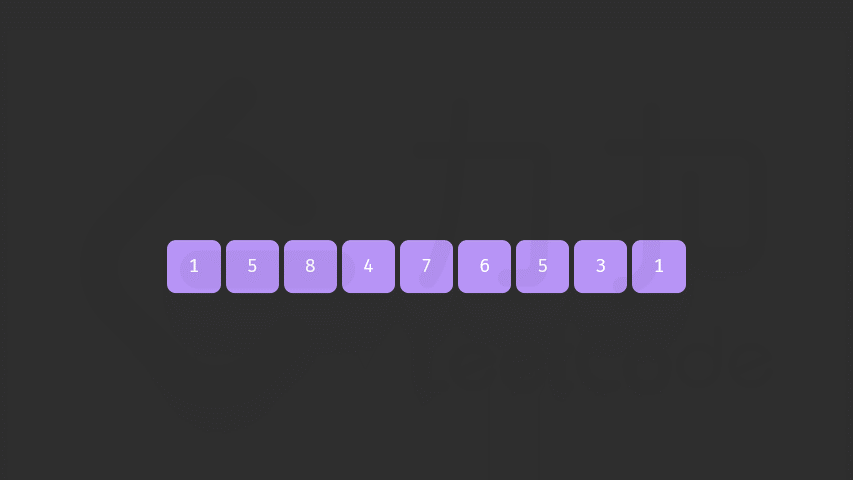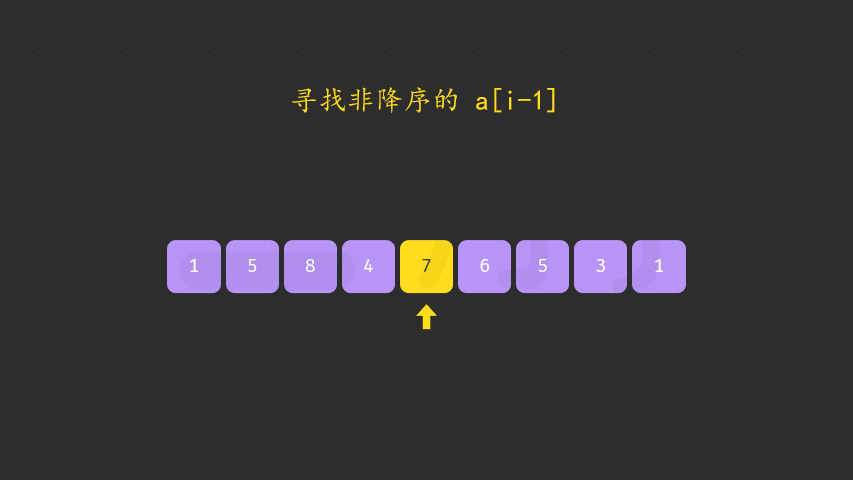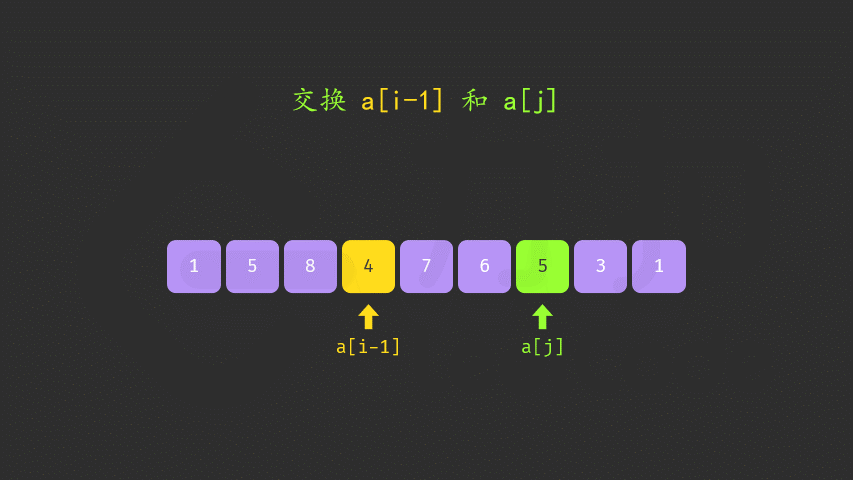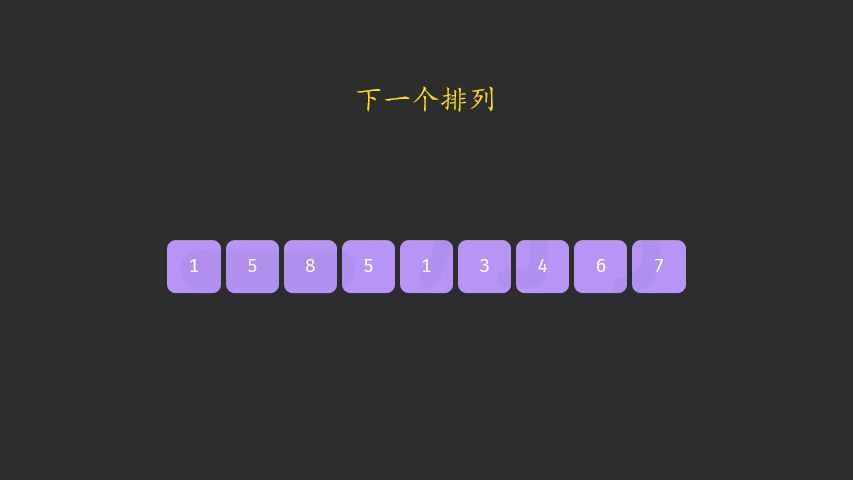(LeetCodeHot100)31. 下一个排列——next-permutation
(LeetCodeHot100)31. 下一个排列——next-permutation
zhangzhang31. 下一个排列——next-permutation
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。 - 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。 - 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
1 | 输入:nums = [1,2,3] |
示例 2:
1 | 输入:nums = [3,2,1] |
示例 3:
1 | 输入:nums = [1,1,5] |
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
前言
本题要求我们实现一个算法,将给定数字序列重新排列成字典序中下一个更大的排列。
以数字序列 [1,2,3] 为例,其排列按照字典序依次为:
[1,2,3][1,3,2][2,1,3][2,3,1][3,1,2][3,2,1]
这样,排列 [2,3,1] 的下一个排列即为 [3,1,2]。特别的,最大的排列 [3,2,1] 的下一个排列为最小的排列 [1,2,3]。
方法一:两遍扫描
思路及解法
注意到下一个排列总是比当前排列要大,除非该排列已经是最大的排列。我们希望找到一种方法,能够找到一个大于当前序列的新序列,且变大的幅度尽可能小。具体地:
- 我们需要将一个左边的「较小数」与一个右边的「较大数」交换,以能够让当前排列变大,从而得到下一个排列。
- 同时我们要让这个「较小数」尽量靠右,而「较大数」尽可能小。当交换完成后,「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下,使变大的幅度尽可能小。
以排列 [4,5,2,6,3,1] 为例:
- 我们能找到的符合条件的一对「较小数」与「较大数」的组合为 2 与 3,满足「较小数」尽量靠右,而「较大数」尽可能小。
- 当我们完成交换后排列变为 [4,5,3,6,2,1],此时我们可以重排「较小数」右边的序列,序列变为 [4,5,3,1,2,6]。
具体地,我们这样描述该算法,对于长度为 n 的排列 a:
- 首先从后向前查找第一个顺序对 (i,i+1),满足 a[i]<a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n) 必然是下降序列。
- 如果找到了顺序对,那么在区间 [i+1,n) 中从后向前查找第一个元素 j 满足 a[i]<a[j]。这样「较大数」即为 a[j]。
- 交换 a[i] 与 a[j],此时可以证明区间 [i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n) 使其变为升序,而无需对该区间进行排序。
注意
如果在步骤 1 找不到顺序对,说明当前序列已经是一个降序序列,即最大的序列,我们直接跳过步骤 2 执行步骤 3,即可得到最小的升序序列。
该方法支持序列中存在重复元素,且在 C++ 的标准库函数 next_permutation 中被采用。
代码
1 | class Solution { |
复杂度分析
- 时间复杂度:O(N),其中 N 为给定序列的长度。我们至多只需要扫描两次序列,以及进行一次反转操作。
- 空间复杂度:O(1),只需要常数的空间存放若干变量。