（LeetCodeHot100）105. 从前序与中序遍历序列构造二叉树——construct-binary-tree-from-preorder-and-inorder-traversal

zhangzhang2025-12-172025-12-19

105. 从前序与中序遍历序列构造二叉树——construct-binary-tree-from-preorder-and-inorder-traversal

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

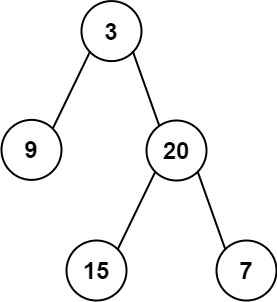
1 2	输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]

示例 2:

1 2	输入: preorder = [-1], inorder = [-1] 输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

第一次写是在学校的PTA里面用c++写的
现在又忘记了，巩固一下：

可以根据先序序列和中序序列的特点，使用递归的方法来构建二叉树。先序序列的第一个元素就是根节点，然后在中序序列中找到根节点的位置，根节点左边的元素就是左子树的中序序列，右边的元素就是右子树的中序序列。根据中序序列中左子树和右子树的节点个数，在先序序列中也可以划分出左子树和右子树的先序序列，然后递归地构建左子树和右子树。

BiTNode* CreateBT(int* pre, int *in, int n) {
    if (n == 0) {
        return NULL;
    }
    // 先序序列的第一个元素为根节点
    BiTNode *root = new BiTNode(pre[0], NULL, NULL);
    int rootIndex;
    // 在中序序列中找到根节点的位置
    for (rootIndex = 0; rootIndex < n; rootIndex++) {
        if (in[rootIndex] == pre[0]) {
            break;
        }
    }
    // 递归构建左子树
    root->lchild = CreateBT(pre + 1, in, rootIndex);
    // 递归构建右子树
    root->rchild = CreateBT(pre + rootIndex + 1, in + rootIndex + 1, n - rootIndex - 1);
    return root;
}

根据c++的答案写的java

由于在 Java 中，int[]（数组）不能直接用 + 运算符进行 “偏移” 操作（比如你代码里的 preorder+1、inorder+rootIndex+1），核心原因是 Java 的数组是引用类型，且没有重载 + 运算符来支持 “指针偏移” —— 这和 C/C++ 完全不同
所以我使用了java里面的数组的工具类：Arrays.copyOfRange() 方法直接抽离数组的「某一段子数组」

1	Arrays.copyOfRange(原数组, 起始索引（包含）, 结束索引（不包含）)

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTree(preorder, inorder, preorder.length);
    }

    private TreeNode buildTree(int[] preorder, int[] inorder, int n) {
        // 当前无结点，返回空
        if (n == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0], null, null);
        int rootIndex;
        // 用先序的第一个去在中序中找该树的根节点的位置
        for (rootIndex = 0; rootIndex < inorder.length; rootIndex++) {
            if (preorder[0] == inorder[rootIndex]) {
                break;
            }
        }
        // 此时中序序列中根节点左边是左子树，右边的是右子树
        root.left = buildTree(Arrays.copyOfRange(preorder, 1, preorder.length), inorder, rootIndex);
        root.right = buildTree(Arrays.copyOfRange(preorder, rootIndex+1, preorder.length), Arrays.copyOfRange(inorder, rootIndex+1,inorder.length), n-rootIndex-1 );
        return root;
    }
}

官方题解

前言

二叉树前序遍历的顺序为：

先遍历根节点；
随后递归地遍历左子树；
最后递归地遍历右子树。

二叉树中序遍历的顺序为：

先递归地遍历左子树；
随后遍历根节点；
最后递归地遍历右子树。

在「递归」地遍历某个子树的过程中，我们也是将这颗子树看成一颗全新的树，按照上述的顺序进行遍历。挖掘「前序遍历」和「中序遍历」的性质，我们就可以得出本题的做法。

方法一：递归

思路

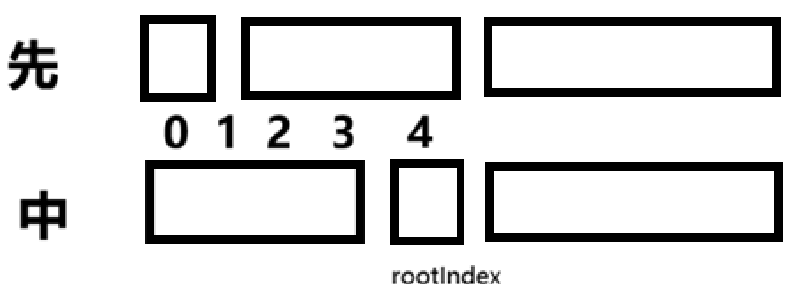
对于任意一颗树而言，前序遍历的形式总是

1	[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

1	[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

细节

在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要 O(1) 的时间对根节点进行定位了。

下面的代码给出了详细的注释。

class Solution {
    private Map<Integer, Integer> indexMap;

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}

复杂度分析

时间复杂度：O(n)，其中 n 是树中的节点个数。
空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，我们还需要使用 O(n) 的空间存储哈希映射，以及 O(h)（其中 h 是树的高度）的空间表示递归时栈空间。这里 h<n，所以总空间复杂度为 O(n)。

方法二：迭代

思路

迭代法是一种非常巧妙的实现方法。

对于前序遍历中的任意两个连续节点 u 和 v，根据前序遍历的流程，我们可以知道 u 和 v 只有两种可能的关系：

v 是 u 的左儿子。这是因为在遍历到 u 之后，下一个遍历的节点就是 u 的左儿子，即 v；
u 没有左儿子，并且 v 是 u 的某个祖先节点（或者 u 本身）的右儿子。如果 u 没有左儿子，那么下一个遍历的节点就是 u 的右儿子。如果 u 没有右儿子，我们就会向上回溯，直到遇到第一个有右儿子（且 u 不在它的右儿子的子树中）的节点 ua*，那么 *v 就是 ua 的右儿子。

第二种关系看上去有些复杂。我们举一个例子来说明其正确性，并在例子中给出我们的迭代算法。

例子

我们以树

为例，它的前序遍历和中序遍历分别为

1 2	preorder = [3, 9, 8, 5, 4, 10, 20, 15, 7] inorder = [4, 5, 8, 10, 9, 3, 15, 20, 7]

我们用一个栈 stack 来维护「当前节点的所有还没有考虑过右儿子的祖先节点」，栈顶就是当前节点。也就是说，只有在栈中的节点才可能连接一个新的右儿子。同时，我们用一个指针 index 指向中序遍历的某个位置，初始值为 0。index 对应的节点是「当前节点不断往左走达到的最终节点」，这也是符合中序遍历的，它的作用在下面的过程中会有所体现。

首先我们将根节点 3 入栈，再初始化 index 所指向的节点为 4，随后对于前序遍历中的每个节点，我们依次判断它是栈顶节点的左儿子，还是栈中某个节点的右儿子。

我们遍历 9。9 一定是栈顶节点 3 的左儿子。我们使用反证法，假设 9 是 3 的右儿子，那么 3 没有左儿子，index 应该恰好指向 3，但实际上为 4，因此产生了矛盾。所以我们将 9 作为 3 的左儿子，并将 9 入栈。
- stack = [3, 9]
- index -> inorder[0] = 4
我们遍历 8，5 和 4。同理可得它们都是上一个节点（栈顶节点）的左儿子，所以它们会依次入栈。
- stack = [3, 9, 8, 5, 4]
- index -> inorder[0] = 4
我们遍历 10，这时情况就不一样了。我们发现 index 恰好指向当前的栈顶节点 4，也就是说 4 没有左儿子，那么 10 必须为栈中某个节点的右儿子。那么如何找到这个节点呢？栈中的节点的顺序和它们在前序遍历中出现的顺序是一致的，而且每一个节点的右儿子都还没有被遍历过，那么这些节点的顺序和它们在中序遍历中出现的顺序一定是相反的。

这是因为栈中的任意两个相邻的节点，前者都是后者的某个祖先。并且我们知道，栈中的任意一个节点的右儿子还没有被遍历过，说明后者一定是前者左儿子的子树中的节点，那么后者就先于前者出现在中序遍历中。

因此我们可以把 index 不断向右移动，并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点，那么说明我们在中序遍历中找到了栈顶节点，所以将 index 增加 1 并弹出栈顶节点，直到 index 对应的元素不等于栈顶节点。按照这样的过程，我们弹出的最后一个节点 x 就是 10 的双亲节点，这是因为 10 出现在了 x 与 x 在栈中的下一个节点的中序遍历之间，因此 10 就是 x 的右儿子。

回到我们的例子，我们会依次从栈顶弹出 4，5 和 8，并且将 index 向右移动了三次。我们将 10 作为最后弹出的节点 8 的右儿子，并将 10 入栈。
- stack = [3, 9, 10]
- index -> inorder[3] = 10
我们遍历 20。同理，index 恰好指向当前栈顶节点 10，那么我们会依次从栈顶弹出 10，9 和 3，并且将 index 向右移动了三次。我们将 20 作为最后弹出的节点 3 的右儿子，并将 20 入栈。
- stack = [20]
- index -> inorder[6] = 15
我们遍历 15，将 15 作为栈顶节点 20 的左儿子，并将 15 入栈。
- stack = [20, 15]
- index -> inorder[6] = 15
我们遍历 7。index 恰好指向当前栈顶节点 15，那么我们会依次从栈顶弹出 15 和 20，并且将 index 向右移动了两次。我们将 7 作为最后弹出的节点 20 的右儿子，并将 7 入栈。
- stack = [7]
- index -> inorder[8] = 7

此时遍历结束，我们就构造出了正确的二叉树。

算法

我们归纳出上述例子中的算法流程：

我们用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点（前序遍历的第一个节点），指针指向中序遍历的第一个节点；
我们依次枚举前序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点，那么我们不断地弹出栈顶节点并向右移动 index，并将当前节点作为最后一个弹出的节点的右儿子；如果 index 和栈顶节点不同，我们将当前节点作为栈顶节点的左儿子；
无论是哪一种情况，我们最后都将当前的节点入栈。

最后得到的二叉树即为答案。

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || preorder.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        stack.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.length; i++) {
            int preorderVal = preorder[i];
            TreeNode node = stack.peek();
            if (node.val != inorder[inorderIndex]) {
                node.left = new TreeNode(preorderVal);
                stack.push(node.left);
            } else {
                while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                    node = stack.pop();
                    inorderIndex++;
                }
                node.right = new TreeNode(preorderVal);
                stack.push(node.right);
            }
        }
        return root;
    }
}