2025-2026-1《数据结构》测验4

选择

1.

数据结构是一门研究非数值计算的程序设计问题中计算机的（）以及它们之间的关系和运算等的学科。

A.操作对象

B.计算方法

C.逻辑存储

D.数据映象

• 数据结构的核心定义是：研究非数值计算的程序设计问题中，计算机的操作对象（如数组、链表、树、图等），以及这些对象之间的逻辑关系、物理存储方式和相关运算（如插入、删除、排序等）

4.

在仅设有尾指针的表长为n的单循环链表中，以下操作时间复杂度为O(n)的是（）。

A.表头插入

B.表头删除

C.表尾插入

D.表尾删除

• 表尾删除要知道表尾指针的前一个，需要先遍历一遍

9.

将森林转换为对应的二叉树，若在二叉树中，结点u是结点v的父结点的父结点，则在原来的森林中，u和v可能具有的关系是( )。
Ⅰ．父子关系 Ⅱ．兄弟关系 Ⅲ．u的父结点与v的父结点是兄弟关系

孩子的孩子

1
2
3
4
5

	u	
   /
  _
 /
v

Ⅰ．父子关系：

1
2
3
4
5

u	
  /
 _
  \
v

兄弟的孩子

1
2
3
4
5

u	
 \
  _
 /
v

Ⅱ．兄弟关系

1
2
3
4
5

u	
 \
  _
   \
	v

12.

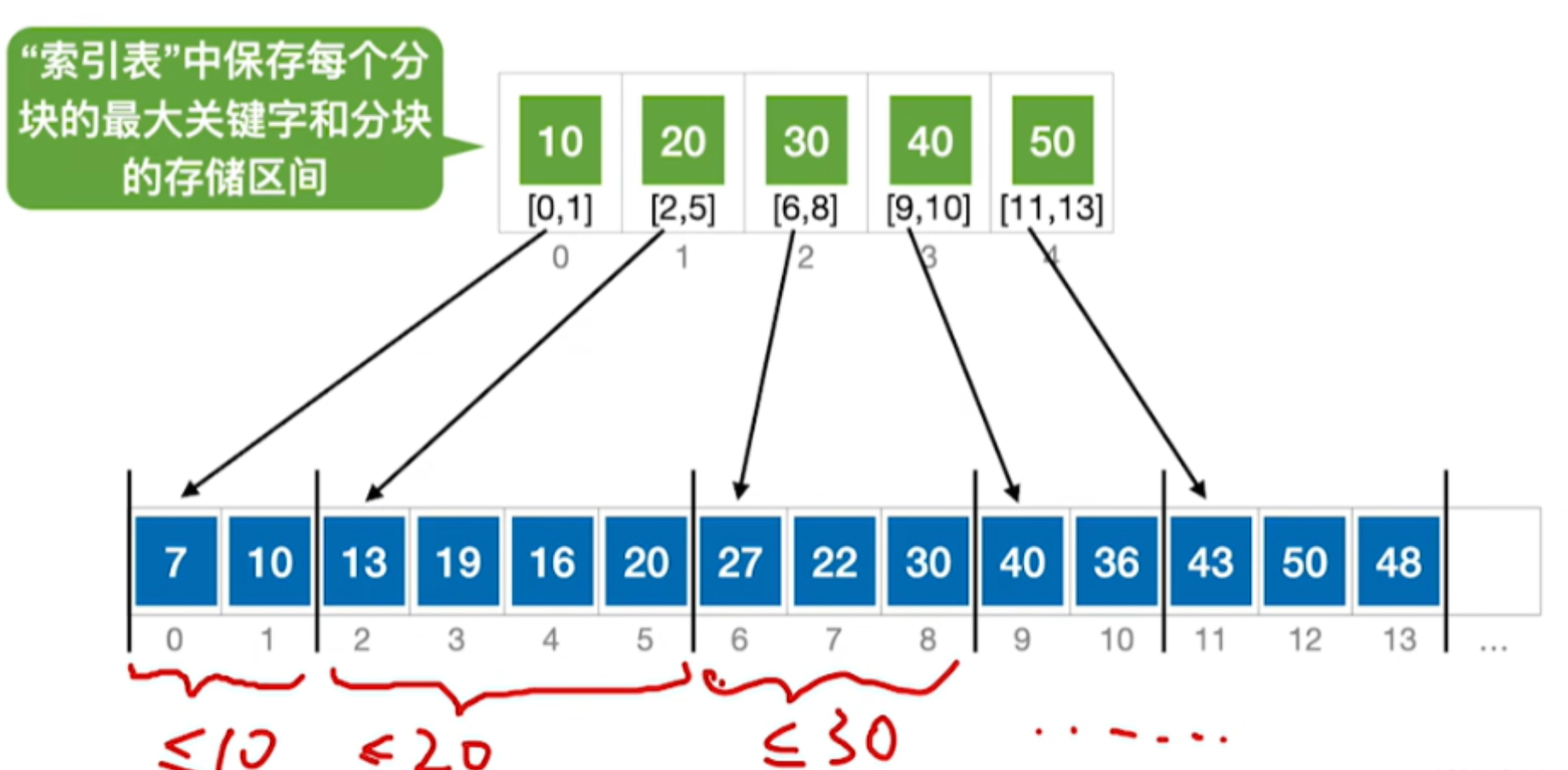
某索引顺序表共有元素395个，平均分成5块。若先对索引表采用顺序查找，再对块中元素进行顺序查找，则在等概率情况下，分块查找成功的平均查找长度是（ ）。

A.43

B.79

C.198

D.200

分块查找的平均查找长度为索引查找和块内查找的平均长度之和。

设索引查找和块内查找的平均查找长度分别为$L_I, L_S$，则分块查找的平均查找长度为：

$$ASL = L_I + L_S$$

我们假设，将长度为$n$的查找表均匀地分为==$b$块==，==每块有$s$个==记录，即$b = n/s$。在等概率情况下，若在块内和索引表中均采用顺序查找，则平均查找长度为：

==$$ ASL = L_I + L_S = \frac{b + 1}{2} + \frac{s + 1}{2} = \frac{s^2 + 2s + n}{2s} $$==

此时，若==$s = \sqrt{n}$==，则平均查找长度取最小值$\sqrt{n} + 1$；

若对索引表采用折半查找时，则平均查找长度为：

==$$ASL = L_I + L_S = \lfloor \log_2(b + 1) \rfloor + \frac{s + 1}{2}$$==

填空

2.

已知关键字序列 { 78，25，30，19，6，130，205，115，39，396，63，337 }，分别用顺序查找、折半查找以及构造二叉排序树、平衡二叉树和散列表来实现查找。

（1）平均查找长度按照最简分数的形式分子/分母填写，分母为1的可以省略分母，只写分子。
（2）如果一个空需要填写多个整数时，按顺序将整数之间用减号(- )连接，首尾及中间均没有空格。例如某个空需要从左到右依次填写1，2，3，4，5，6共6个整数，则填写1-2-3-4-5-6即可。

（1）顺序查找

对上述关键字序列进行顺序查找，请问：

• 在等概率情况下查找成功时的平均查找长度为（13/2）；
• 查找关键字70需要和关键字比较（==13==）次才能确定不存在。

答案是13次，搞不懂，12个数不应该是比较12次吗

懂了：顺序查找不成功的次数就是n+1，就比如数组下标从0到n-1，遍历到i=n时，才确定查找失败

（2）折半查找

若上述关键字序列是已从小到大排好序的，采用折半查找，画出折半查找判定树，请问：

• 对折半查找判定树树根的左子树进行先序遍历，得到的关键字先序遍历序列是（25-6-19-30-39）；
• 在等概率情况下查找成功时的平均查找长度为（37/12）；
• 查找关键字70需要依次和哪些关键字比较才能确定不存在（63-130-78）。

（3）二叉排序树

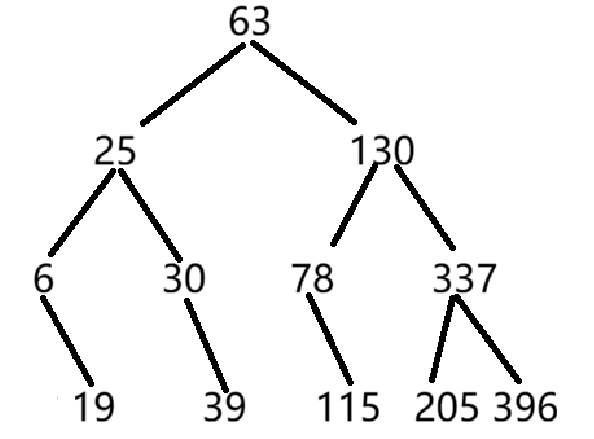
用上述关键字序列构造二叉排序树，请问：

• 构造的二叉排序树的高度是（5）；
• 在构造的二叉排序树中，查找关键字396需要依次和哪些关键字比较（不包括关键字396）（78-130-205）；
• 在构造的二叉排序树中，查找关键字70需要依次和哪些关键字比较才能确定不存在（78-25-30-39-63）；
• 在等概率情况下查找成功时的平均查找长度为（13/4）；
• 在等概率情况下查找不成功时的平均查找长度为（51/13）。（有多少种不可能就除以几）

（4）平衡二叉树

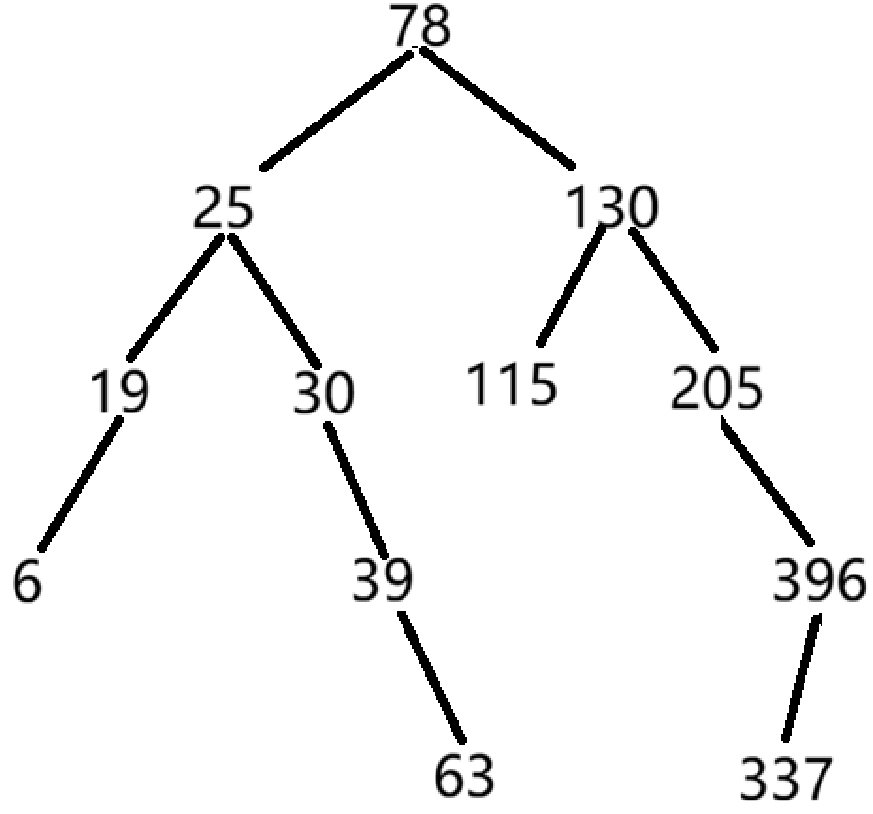
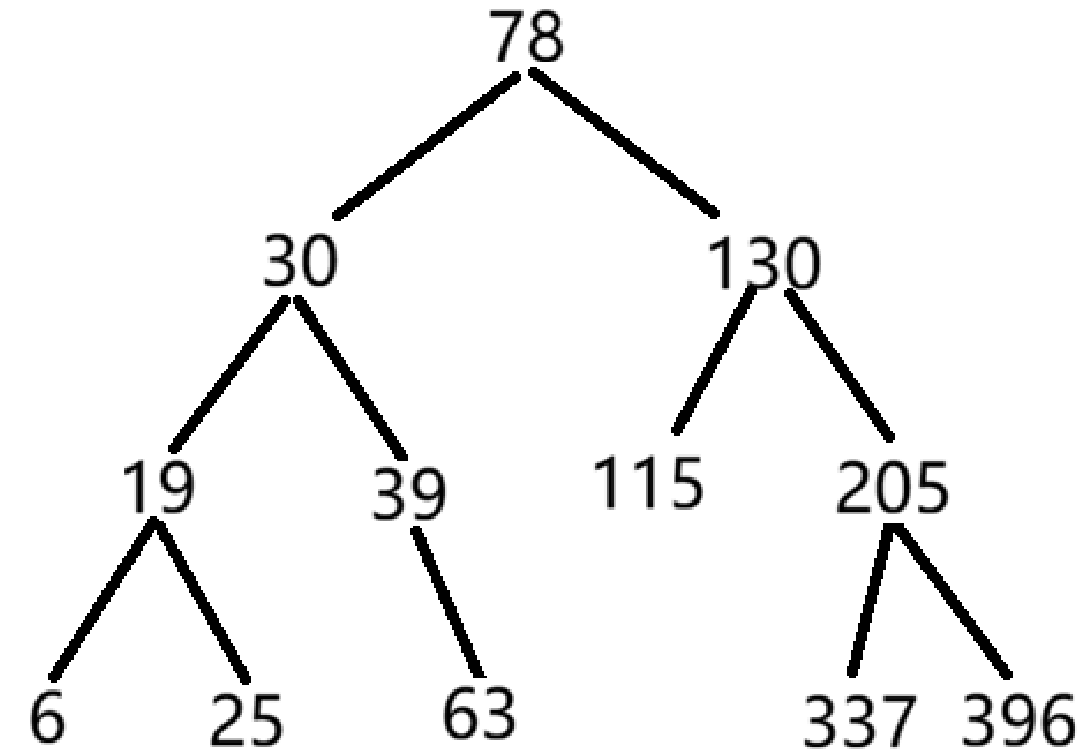
用上述关键字序列构造平衡二叉树，请问：

• 在构造平衡二叉树过程中共需要经过（5）次平衡化处理；
• 构造的平衡二叉树的高度是（4）；
• 在构造的平衡二叉树中，平衡因子等于0的非终端结点有（4）个；
• 在构造的平衡二叉树中，查找关键字396需要依次和哪些关键字比较（不包括关键字396）（78-130-337）；
• 在构造的平衡二叉树中，查找关键字70需要依次和哪些关键字比较才能确定不存在（78-30-39-63）；

（5）散列表

用上述关键字序列构造散列表，散列表的地址空间为A[0…14]，哈希函数采用除留余数法设计，处理冲突的办法采用线性探测再散列法。请问：

• 在散列表中查找关键字396需要依次和哪些关键字比较（不包括关键字396）（19-6）；
• 在散列表中查找关键字51需要依次和哪些关键字比较才能确定不存在（25-63-337-78-130-39）；
• 散列表地址空间中，空的没有填写关键字的地址下标（从小到大）依次是（3-5-9）；
• 在等概率情况下查找成功时的平均查找长度是（11/6）；
• 在等概率情况下查找不成功时的平均查找长度是（34/13）（计算不成功时的平均查找长度时只考虑和关键字比较的次数）。

散列表

==散列表表长为m，取一个不大于m但最接近或等于m的质数p==

m=15,H(key)=key(mod13)，线性探测。

1. 查找 396 比较的关键字：H(396)=6，地址 6(19), 7(6), 找到地址 8。排除自身后为 19-6。
2. 查找 51 确定不存在的比较序列：H(51)=12，地址 12(25), 13(63), 14(337), 0(78), 1(130), 2(39), 3(空)。序列为 25-63-337-78-130-39。
3. 空地址下标：从小到大依次是 3-5-9。
4. 查找成功的平均查找长度：121+1+1+1+2+2+1+1+3+3+3+3=22/12=11/6。
5. 查找不成功的平均查找长度（算只算前13个）：针对 H(k)∈[0,12] 的 13 种情况：(3+2+1+0+1+0+3+2+1+0+8+7+6)/13=34/13。

函数

3-1 递增的整数序列链表的插入

分数 5

作者 DS课程组

单位 浙江大学

本题要求实现一个函数，在递增的整数序列链表（带头结点）中插入一个新整数，并保持该序列的有序性。

函数接口定义：

1

List Insert( List L, ElementType X );

其中List结构定义如下：

1
2
3
4
5
6

typedef struct Node *PtrToNode;
struct Node {
    ElementType Data; /* 存储结点数据 */
    PtrToNode   Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */

L是给定的带头结点的单链表，其结点存储的数据是递增有序的；函数Insert要将X插入L，并保持该序列的有序性，返回插入后的链表头指针。

裁判测试程序样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#include <stdio.h>
#include <stdlib.h>

typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
    ElementType Data;
    PtrToNode   Next;
};
typedef PtrToNode List;

List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表 */

List Insert( List L, ElementType X );

int main()
{
    List L;
    ElementType X;
    L = Read();
    scanf("%d", &X);
    L = Insert(L, X);
    Print(L);
    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：

1
2
3

5
1 2 4 5 6
3

输出样例：

1

1 2 3 4 5 6 

我居然忘记移动指针了

正确答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

List Insert(List L, ElementType X) {
    List p = L;  // 从表头开始遍历（更灵活）
    
    // 找到插入位置：p的下一个节点值大于X，或p是最后一个节点
    while (p->Next != NULL && p->Next->Data < X) {
        p = p->Next;
    }
    
    // 此时p就是要插入的前一个节点，统一处理所有插入情况
    List newNode = (List)malloc(sizeof(struct Node));
    newNode->Data = X;
    newNode->Next = p->Next;  // 新节点指向p原来的下一个节点
    p->Next = newNode;        // p指向新节点
    
    return L;
}

3-2 确定二叉树（先序序列+中序序列）

分数 5

作者 黄龙军

单位 绍兴文理学院

要求实现函数，根据二叉树的先序序列和中序序列确定二叉树并返回指向二叉树根结点的指针。二叉树采用二叉链表存储，结点结构如下：

1
2
3
4
5
6
7
8
9

struct BiTNode {                                  // 结点结构 
    int data;                                     // 数据域 
    BiTNode *lchild,*rchild;                      // 左右孩子指针 
    BiTNode(int d,BiTNode *left,BiTNode *right) { // 构造函数 
        data=d;
        lchild=left;
        rchild=right;
    }
};

函数接口定义：

1

BiTNode* CreateBT(int* pre, int *in, int n);

其中参数 pre是指向先序序列数组首元素的指针， in是指向中序序列数组首元素的指针 ，n是结点总数。

裁判测试程序样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

#include<iostream>
using namespace std;

struct BiTNode {                                  // 结点结构 
    int data;                                     // 数据域 
    BiTNode *lchild,*rchild;                      // 左右孩子指针 
    BiTNode(int d,BiTNode *left,BiTNode *right) { // 构造函数 
        data=d;
        lchild=left;
        rchild=right;
    }
};

void PostOrder(BiTNode* p, int &cnt)    // 后序遍历
//  根据先序序列和中序序列确定二叉树，pre是指向后序序列数组首元素的指针，in是指向中序序列数组首元素的指针 ，n是结点总数
BiTNode* CreateBT(int* pre, int *in, int n);  

// 根据先序序列和中序序列创建二叉树并后序遍历之
int main() {
    int n;
    while(cin>>n) {
        int pre[n], in[n], cnt=0;
        for(int i=0; i<n; i++) cin>>pre[i];
        for(int i=0; i<n; i++) cin>>in[i];
        BiTNode* root=CreateBT(pre,in,n);
        PostOrder(root, cnt);
        cout<<endl;
    }
    return 0;
}

//请在此处填写答案

void PostOrder(BiTNode* p, int &cnt) {                 // 后序遍历
    if(!p) return;
    PostOrder(p->lchild, cnt);
    PostOrder(p->rchild, cnt);
    cnt++;
    if (cnt>1) cout<<" ";
    cout<<p->data;
}

输入样例：

1
2
3

9
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6

输出样例：

1

7 4 2 8 9 5 6 3 1

我的答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

BiTNode* CreateBT(int* pre, int *in, int n) {
    if (n == 0) {
        return NULL;
    }
    int index;
    for (index=0; index<in.length(); index++) {
    	if (pre[0] == in[index]) {
    		break;
		}
	}
    BiTNode *p = new BiTNode(pre[0],NULL,NULL);
    p.lchild = CreateBT(pre+1,in,index);
    p.rchild = CreateBT(pre+1+index,in+1+index,n-index-1);
    return p;
}

• 参数给了n

• C++ 中不能直接用 in.length()，核心原因是：in 是 int* 类型（指向数组的指针），而指针没有 length() 成员函数

与java区别

数组名和指针

所以说数组名不是指针

• arr 是 “数组类型的常量标识”，p 是 “指针类型的变量”；arr 会在多数场景下「隐式转换成 p 的类型」，但转换后就不是 arr 本身了。

1.先看 “看起来一样” 的场景（隐式转换后的行为一致）

这是你觉得 “arr 就是 p” 的核心原因 —— 数组名 arr 会自动转成指向首元素的指针，此时两者的用法完全相同：

1
2
3
4
5
6
7
8
9

int arr[5] = {1,2,3,4,5};
int* p = arr;  // arr 隐式转成 int*，赋值给 p

// 1. 访问元素：语法和结果完全一致
cout << arr[2] << " " << p[2];        // 输出 3 3
cout << *(arr+2) << " " << *(p+2);    // 输出 3 3

// 2. 取地址：arr 和 &arr[0] 都是首元素地址，和 p 存储的地址相同
cout << arr << " " << &arr[0] << " " << p;  // 输出同一个地址（如 0x7ffeefbff5a0）

此时的 arr，在表达式中确实 “表现得像 p”，但这只是「隐式转换后的表象」，不是本质。

2.再看 “本质不同” 的场景（暴露核心差异）

只要脱离 “访问元素” 这个场景，两者的区别立刻显现：

(1) sizeof 结果完全不同（最直观）

sizeof 是编译时运算符，直接作用于变量的「原始类型」，而不是转换后的类型：

1
2

cout << sizeof(arr);  // 输出 20（5个int，每个4字节：5×4=20）—— arr的原始类型是 int[5]
cout << sizeof(p);    // 输出 8（64位系统）或4（32位系统）—— p的原始类型是 int*（指针）

• arr 携带长度信息，所以 sizeof(arr) 计算的是「整个数组的总字节数」；
• p 只存储地址，所以 sizeof(p) 计算的是「指针变量本身的字节数」，和数组长度无关。

(2) arr 不能赋值，p 可以赋值

arr 是「数组的常量标识」，它的 “指向” 是固定的（不能改变它对应的数组）；而 p 是「指针变量」，可以随时修改指向：

1
2
3
4

int brr[5] = {6,7,8,9,10};

// arr = brr;  // 错误！arr 是常量，不能赋值（不能让它指向 brr 数组）
p = brr;       // 正确！p 是变量，现在指向 brr 的首地址，p[2] 会输出 8

正确答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

BiTNode* CreateBT(int* pre, int *in, int n) {
    if (n == 0) {
        return NULL;
    }
    // 先序序列的第一个元素为根节点
    BiTNode *root = new BiTNode(pre[0], NULL, NULL);
    int rootIndex;
    // 在中序序列中找到根节点的位置
    for (rootIndex = 0; rootIndex < n; rootIndex++) {
        if (in[rootIndex] == pre[0]) {
            break;
        }
    }
    // 递归构建左子树
    root->lchild = CreateBT(pre + 1, in, rootIndex);
    // 递归构建右子树
    root->rchild = CreateBT(pre + rootIndex + 1, in + rootIndex + 1, n - rootIndex - 1);
    return root;
}